Съдържание

• инструкции
• съвети
• Какво ви трябва

Разбирането на математическия процес при изчисляването на обема на трапецоида преминава през сърцето на геометрията на концептуалното и практическото научно конструиране. Текстът по-долу е стъпка по стъпка, за да се разберат първо основните принципи, които съпровождат променливите на същественото формулирано уравнение, и след това да се използва за решаване на проблеми с трапецовидни фигури.

инструкции

Разбирането на математическия процес при изчисляване на обема на трапецоида преминава през сърцето на геометрията на концептуалното и практическото научно строителство. (математическо изображение от jaddingt от Fotolia.com)

1. Разбирането, че изграждането на практически проекти, като жилищни или търговски сгради, почвени работи като кални легла и къщи и други съоръжения, включват необходимите познания за обема на течните вещества в затворени плоски фигури, което ще позволи на ученика да разбиране на необходимостта от изчисляване на обема. Точното измерване на съществуващите размери води до точно изчисление на обема.

   На практика, намирането на трапецовидни сечения на глинени стени в географския басейн е полезно при определяне на трапецовидност. Ако две страни на четиристранна фигура са успоредни, но не са равни по размер, а другите две страни не са успоредни, тази цифра се нарича трапецовидна.

   
   

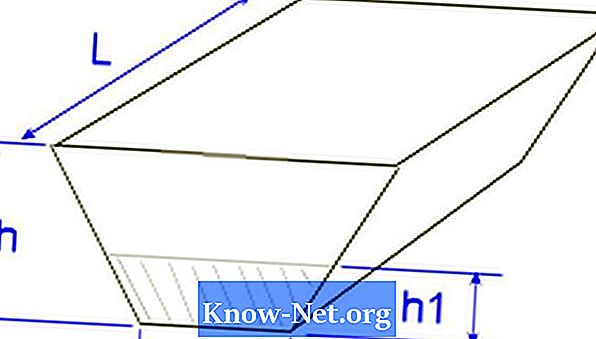
   Така че, ако имате фигура с дължина 22,86 м, размерът на предната част е широк 17,37 м и висок 10,66 м и има дъно с ширина 21,94 м и 3,65 м височината, изчислете обема, както следва:

   1. Формата може да се разглежда като правоъгълник от 17,37 x 22,86 отпред, прикрепен към равнини от 21,94 x 3,65 на дъното, на разстояние 22,86 m;

   2. Формулата за изчисляване на обема по този начин, която може да бъде начертана като ствол с правоъгълен връх и дъно вместо предната и задната, може да се изрази като V = [a1]b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3, където променливите могат да бъдат описани с a1 = 17,37; b1 = 10.66; a21D = 21,94; b2 = 3,65; h = 22.86: V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3 V = [17.3710,66 + 21,943,65 + (17,373,65 + 21,9410.66) / 2] * 22.86 / 3 V = [265.60 + (63.54 + 234.11) / 2] * 7.62 V = [265.60 + (297.66) / 2 ] 7,62 V = [414,44] 7.62 V = 3158.03 m³

2. Следвайки формата, динамичният обем на трапеца се различава от този на статичния модел, защото статичният трапец е геометрично двуизмерен. Площта, която трябва да се изчисли, може да бъде само на трапецовидна форма, начертана в две измерения на хартия. Следователно, алтернативна версия на формулата, използвайки средната ширина и дължина е: V = [a1b1 + a2b2 + 4 ((a1 + a2) / 2 * (b1 + b2) / 2)] * h / 6 Правоъгълникът има страни, които са средните страни на горния и долния правоъгълник.

   
   

3. Действайки както при динамичното прилагане на стъпка 2, обемът на трапецовидна конструкция, като например басейн или затворен цилиндър, може да бъде изчислен като литри на метър с определена височина. Това означава, че обемът на пълен контейнер, разделен на неговата височина, дава правилното съотношение - използвайте формулата (с размери в m), за да получите кубични метри.

   За всеки контейнер, който не е цилиндричен, съотношението ще варира с дълбочина, ако студентът желае. Може да се мисли, че това означава, че контейнерът ще бъде частично пълен и че обемът ще бъде определен на различни нива. Това означава, че обемът е функция на височината.

4. Отиваме малко по-нататък, тъй като ширината в посока „а” се променя линейно от a1 на a2, a = a1 + (a2-a1) k = (1-k) a1 + ka2; към кои единици kh се издига от дъното (където k варира от 0 до 1); по същия начин, b = b1 + (b2-b1) k = (1-k) b1 + kb2; обемът на твърдото тяло с височината kh, основата a1 от b1 и горната a by b е V (k) = [a1]b1 + ab + a1b / 2 + ab1 / 2] * kh / 3.

   Ако използваме реалното ниво на течността вместо съотношението k, можем да заместим k = L / h и да получим V (L) = [(3h ^ 2-3Lh + L ^ 2) a1b1 + L2a2a2b2 + (3Lh-2L2) (а1b2 + a2b1) / 2] * L / (3h ^ 2). Това ни дава обем като функция на дълбочината.

5. Изчисляването на обема на трапецоида правилно включва способността да се интерпретира дали трапецовидната фигура е двуизмерна или триизмерна. Динамичната практика на инженерния аспект на трапецоидалната интерпретация се върти около това дали трапецовидната фигура е нещо, което е просто нарисувано или конструирано, независимо дали съдържа обем или просто скица на хартия.

съвети

• Решаването на геометричен проблем позволява на ученика да разбере как и защо формулата е такава и защо височината е толкова важна променлива. Проверка на отговора, получен ръчно с, например, научен калкулатор на Hewlett-Packard, е добър начин за постигане на пълна точност.

Какво ви трябва

• молив
• Лист на бележника (с или без линии)
• владетел